27. 矩阵转置
矩阵转置
有几个卡尔曼滤波器方程需要矩阵转置。这些矩阵很好识别,因为它们都有T上标。例如,矩阵 \mathbf{A} 的转置为 \mathbf{A^T}
下面是三个包含矩阵转置的方程:
\mathbf{P_{k|k-1}} = \mathbf{F_{k}} \mathbf{P_{k-1|k-1}} \mathbf{F_{k}^T} + \mathbf{Q_{k}}
\mathbf{S_{k}} = \mathbf{H_{k}} \mathbf{P_{k|k-1}} \mathbf{H_{k}^T} + \mathbf{R_{k}}
\mathbf{K_{k}} = \mathbf{P_{k|k-1}} \mathbf{H_{k}^T} \mathbf{S_{k}}^{-1}
转置究竟是什么?
你可以将转置视为切换行和列,从而把矩阵行变成列,或者列编程行。
下面是一个例子。对这个矩阵,
\begin{bmatrix}3 & 25 & 9 & 2 & 4 \\ 7 & 15 & 6 & 92 & 17 \\31 & 18 & 0 & 11 & 8\end{bmatrix}
转置结果为
\begin{bmatrix}3 & 7 & 31 \\ 25 & 15 & 18 \\ 9 & 6 & 0 \\ 2 & 92 & 11 \\ 4 & 17 & 8\end{bmatrix}
原始矩阵大小为 3x5。转置后为 5x3。
下面,我们讲解一下具体步骤。这个图像的颜色编码可以匹配原始矩阵的值和转置矩阵的值。把行转换为列之后,矩阵操作如下:
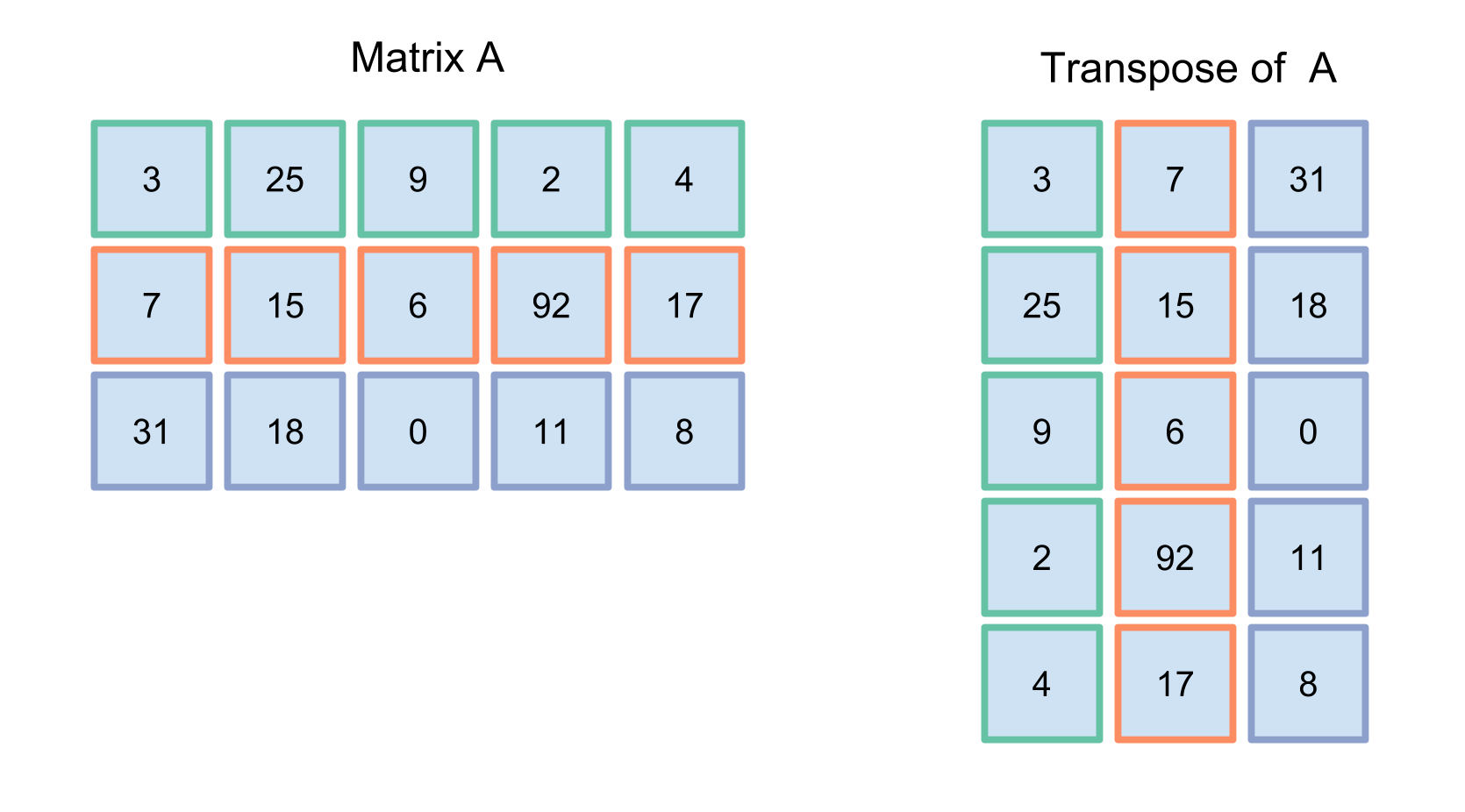
你也可以把转置看成将列转为行:
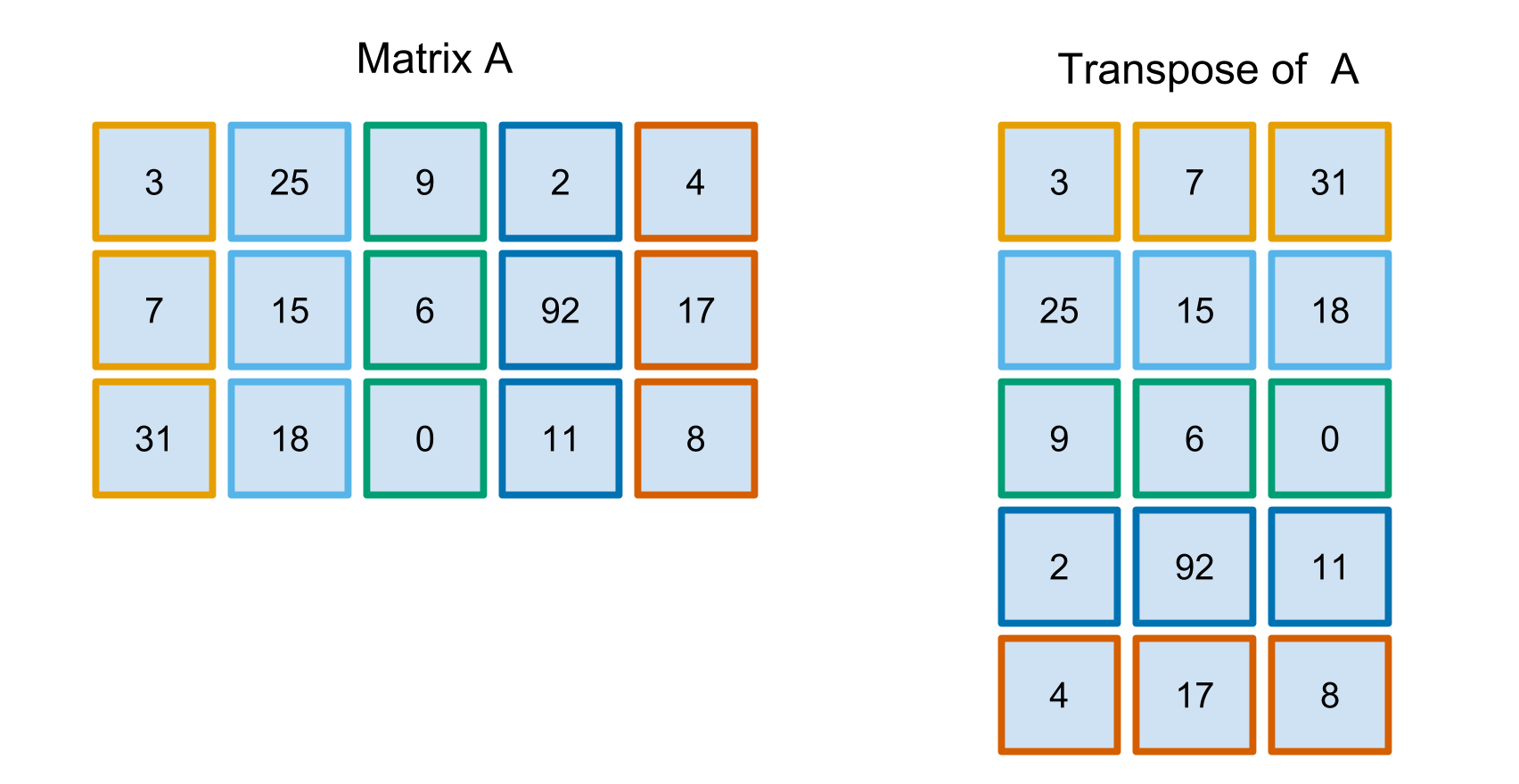
在数学上,你正在转换矩阵中每个元素的 i 和 j 值。例如,第三行第四列的元素是 11。矩阵转置后,11 现在位于第四行第三列。矩阵转置的正式数学定义是
[\mathbf{A^T}]_{ij} = [\mathbf{A}]_{ji}
转置计算的用途
要使用卡尔曼滤波器方程,你需要计算 \mathbf{F} \text{ and } \mathbf{H} 矩阵的转置。
矩阵转置还有另外一个用途:矩阵乘法。在以前的矩阵乘法练习中,你编写过一个返回矩阵列的函数。矩阵列可以帮助我们找到矩阵 \mathbf{A} 中的一行和矩阵 \mathbf{B} 中一列的点积。
结果应该是这样的:

如果取矩阵 \mathbf{B} 的转置,结果如何? \mathbf{B} 中所有列变为行。然后,矩阵乘法函数需要计算 \mathbf{A} 的行和 \mathbf{B^T} 的行的卷积:
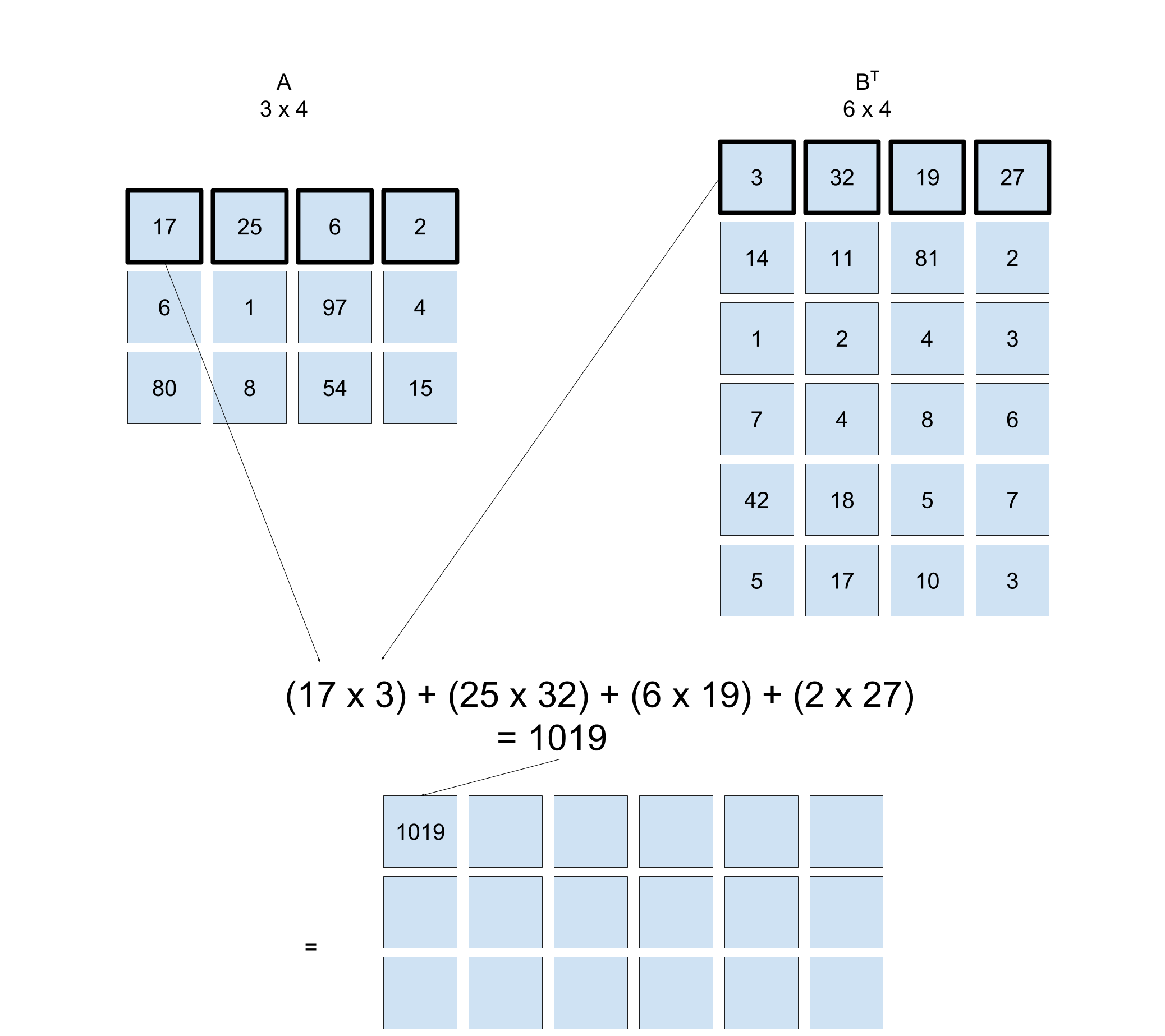
Dot product between rows of A and transpose of matrix B
你计算的不是 AB^T 的乘积。你正在利用矩阵转置来让矩阵乘法的编程更容易。
在前面的编码练习中,将矩阵列转换为水平向量的get_column 函数本质上是一个转置。
在这部分课程的编码练习中,你不仅要编写转置函数,还要编写一个利用矩阵转置的新乘法函数。
矩阵转置编程
这个问题和前面碰到的类似。你需要使用嵌套循环。但这个嵌套循环应该是什么样的呢?
你可以遍历整个矩阵,就像遍历外循环中的行和内循环中的列一样:
for i in range(len(matrixA)):
for j in range(len(matrixA[0])):
print(matrixA[i][j])矩阵的转置将需要将每个 i、j 元素存储在新矩阵的 j、i 位置上。但如何填充这个新的矩阵?首先,你需要在列表中创建一个 n x m 的列表,并用空值填充此嵌套列表。这听起来有点复杂。
有没有更有效的方法来进行矩阵转置编程?你可以考虑一下,如先遍历外部 for 循环中的列和内部 for 循环中的行。
在本课的下一部分有代码编写练习。